数学建模算法：AHP层次分析法

💡AHP层次分析法是什么
层次分析法 (Analytic Hierarchy Process, AHP) 是一种结构化的决策方法，由美国运筹学家托马斯·萨蒂 (Thomas L. Saaty) 教授于 20 世纪 70 年代提出。它将复杂的决策问题分解成多个层次，并通过两两比较的方式确定各个因素的相对重要性，最终得出综合评价结果。AHP 特别适用于那些难以完全定量分析、涉及多个准则和方案的复杂决策问题。
AHP 的核心思想: 将复杂问题层次化、将定性问题定量化。

💡AHP 的具体分析步骤
1️⃣ 建立层次结构模型
2️⃣ 构造判断矩阵 (Pairwise Comparison Matrix)
3️⃣ 计算权重向量和一致性检验：在构建判断矩阵时，有可能会出现逻辑性错误，比如A比B重要，B比C重要，但却又出现C比A重要。因此需要使用一致性检验是否出现问题。为了检验判断矩阵的一致性，需要计算一致性指标 (Consistency Index, CI) 和一致性比率 (Consistency Ratio, CR)。CR值小于0.1则说明通过一致性检验，反之则说明没有通过一致性检验。
4️⃣ 计算综合权重：将方案层相对于每个准则的权重与该准则相对于目标的权重相乘，然后将各个准则的结果相加，得到每个方案的综合权重。
5️⃣ 做出决策：根据方案的综合权重进行排序，选择综合权重最高的方案作为最终决策。

⭐ 例子：选择旅行目的地

假设你计划一次旅行，有三个目的地可供选择：A、B 和 C。你需要考虑以下四个因素：

■ 旅游成本 (Cost)
■ 景点吸引力 (Attractions)
■ 住宿条件 (Accommodation)
■ 餐饮质量 (Food)

就可以用层次分析法来建模，做出决策

先做准则层中旅游成本、景点吸引力、住宿条件、餐饮质量的判断矩阵，得到准则层权重

之后分别针对三个目的地 A、B、C，构建关于每个因素的判断矩阵。以旅游成本为例，比较 A、B、C 三地的花费高低。

将之前得到的准则层各因素权重，与每个目的地在相应因素下的权重进行综合运算。把目的地 A 在旅游成本、景点吸引力、住宿条件、餐饮质量上的得分，分别乘以对应的准则层权重，再相加求和，得到目的地 A、B 和 C 的综合得分。

AHP层次分析法是什么

层次分析法 (Analytic Hierarchy Process, AHP) 是一种结构化的决策方法，由美国运筹学家托马斯·萨蒂 (Thomas L. Saaty) 教授于 20 世纪 70 年代提出。它将复杂的决策问题分解成多个层次，并通过两两比较的方式确定各个因素的相对重要性，最终得出综合评价结果。AHP 特别适用于那些难以完全定量分析、涉及多个准则和方案的复杂决策问题。

AHP 的核心思想: 将复杂问题层次化、将定性问题定量化。

AHP 的具体分析步骤

AHP 的主要步骤可以概括为以下几个方面：

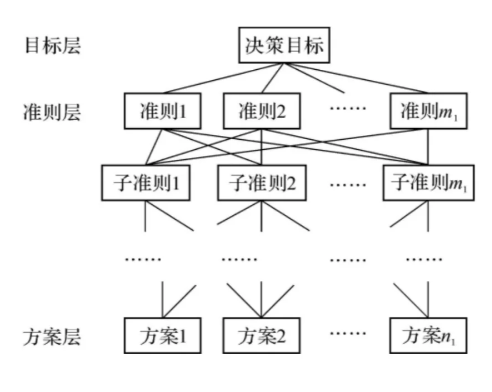
1. 建立层次结构模型:

目标层 (Goal): 决策的最终目标，位于层次结构的顶层。
准则层 (Criteria): 影响决策的各个因素或标准，位于中间层。
方案层 (Alternatives): 可供选择的方案或选项，位于底层。

将问题分解成上述三个层次，并绘制出层次结构图。

举例：选择最佳旅游目的地，需要考虑旅游成本、旅游景点吸引力、住宿条件、餐饮质量等方面，可以利用层次分析法建模，为不同准则层设计不同权重，为不同旅游目的地计算综合得分，最终根据得分来进行选择：

建模：

目标层（A）

选择最佳旅游目的地。

准则层（B）

包括旅游成本（B1）、旅游景点吸引力（B2）、住宿条件（B3）、餐饮质量（B4）这 4 个准则。

方案层（C）

假设有三个旅游目的地可供选择，分别是城市甲（C1）、城市乙（C2）和城市丙（C3）
1
2
3
4
5
6
graph TD
    A[选择最佳旅游目的地]
    A --> B1[旅游成本]
    A --> B2[旅游景点吸引力]
    A --> B3[住宿条件]
    A --> B4[餐饮质量]

2. 构造判断矩阵 (Pairwise Comparison Matrix):

针对每个准则，对方案层中的各个方案进行两两比较，确定它们相对于该准则的相对重要性。
针对目标层，对准则层中的各个准则进行两两比较，确定它们对目标的重要性程度。

比较结果通常使用 Saaty 提出的 1-9 标度方法表示：

标度	含义
1	两元素同等重要
3	元素 i 比元素 j 稍微重要
5	元素 i 比元素 j 明显重要
7	元素 i 比元素 j 强烈重要
9	元素 i 比元素 j 极端重要
2,4,6,8	上述两相邻判断的中值
倒数	元素 i 与 j 的比较，和 j 与 i 相反

将比较结果填入判断矩阵 A 中，其中 $a_{ij}$ 表示元素 i 相对于元素 j 的重要性程度。判断矩阵具有以下性质：
- $a_{ij} > 0$
- $a_{ij} = 1/a_{ji}$ (互反性)
- $a_{ii} = 1$ (自身比较)

3. 计算权重向量和一致性检验:

计算权重向量: 计算每个判断矩阵的特征向量和最大特征值 ( $\lambda_{max}$ )，并将特征向量进行归一化处理，得到各元素相对于上一层级因素的权重。
- 计算特征向量可以用几何平均法、算术平均法或者直接用求解特征值法计算。
- 最大特征值的计算公式
  $λ_{max} = (1/n)∑_{i=1}^{n} (Aw)_{i}/w_{i}$
一致性检验: 在构建判断矩阵时，有可能会出现逻辑性错误，比如A比B重要，B比C重要，但却又出现C比A重要。因此需要使用一致性检验是否出现问题。为了检验判断矩阵的一致性，需要计算一致性指标 (Consistency Index, CI) 和一致性比率 (Consistency Ratio, CR)。CR值小于0.1则说明通过一致性检验，反之则说明没有通过一致性检验。
- 一致性指标 (CI): $CI = \frac{\lambda_{max} - n}{n - 1}$ ，其中 n 是判断矩阵的阶数。
- 一致性比率 (CR): $CR = \frac{CI}{RI}$ ，其中 RI 是随机一致性指标 (Random Index)，其值与判断矩阵的阶数有关，可通过查表获得。
  
  n 1 2 3 4 5 6 7 8 9
  
  RI 0 0 0.52 0.89 1.12 1.24 1.32 1.41 1.45
- 判断标准: 通常认为，当 $CR < 0.1$ 时，判断矩阵具有满意的一致性；否则，需要调整判断矩阵，直到满足一致性要求。

n	1	2	3	4	5	6	7	8	9
RI	0	0	0.52	0.89	1.12	1.24	1.32	1.41	1.45

4. 计算综合权重:

将方案层相对于每个准则的权重与该准则相对于目标的权重相乘，然后将各个准则的结果相加，得到每个方案的综合权重。

5. 做出决策:

根据方案的综合权重进行排序，选择综合权重最高的方案作为最终决策。

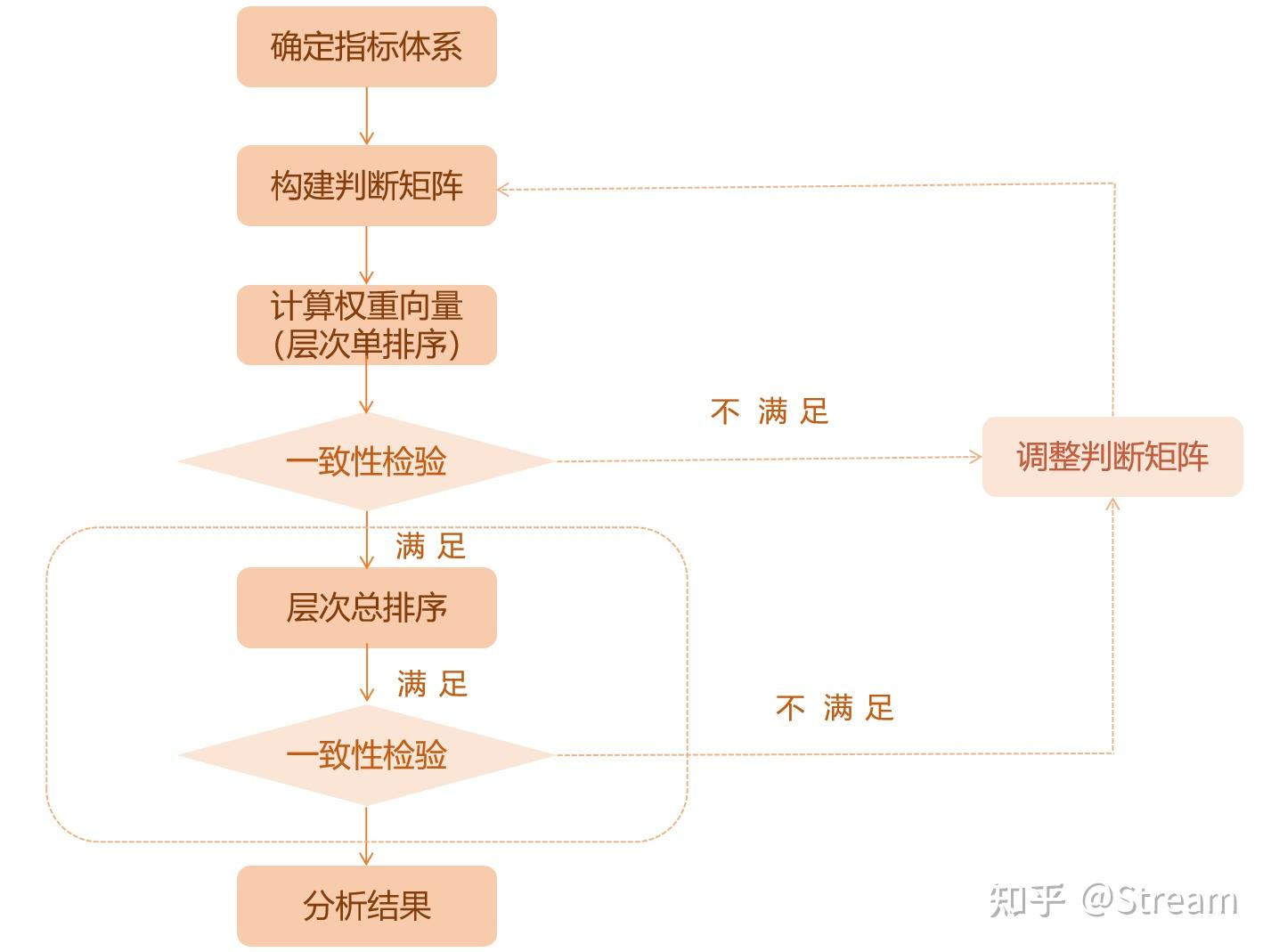
计算步骤流程图：

‍

特征向量、最大特征根、一致性比率怎么计算

特征向量

特征向量是用于表示判断矩阵中各个元素相对重要性的向量。计算特征向量的步骤如下：

构造判断矩阵：假设判断矩阵为 $A$ ，其中 $A_{ij}$ 表示元素 $i$ 与元素 $j$ 的相对重要性。
计算特征向量：

AHP层次分析法中特征向量的计算方法有几何平均法、算术平均法和特征值法。
- 方法1：几何平均法
  1. 计算每行所有元素的乘积
    $M_i = ∏_{j=1}^n a_{ij} (i = 1,2,...,n)$
  2. 计算每行乘积的n次方根，这相当于计算几何平均数。
    $W_i = \sqrt[n]{M_i}$
  3. 归一化处理： 将得到的 n 个几何平均数进行归一化处理，使其和为 1。归一化得到的结果为各特征向量。
    $w_i = W_i / ∑_{k=1}^n W_k$
- 方法2：算术平均法
  1. 计算每列所有元素的和
    $S_j = ∑_{i=1}^n a_{ij} (j = 1,2,...,n)$
  2. 归一化列向量： 对于比较矩阵的每一列 j，将其所有元素除以该列元素的和，得到一个归一化的列向量。
    $a'_{ij} = a_{ij}/S_j$
  3. 计算每行元素的平均值： 对于矩阵的每一行 i，计算该行所有元素的平均值。得到的结果为特征向量。
    $w_i = (1/n)∑_{j=1}^n a'_{ij}$
- 方法3：特征值法
  
  见线性代数中的特征值和特征向量，计算比较复杂，一般写代码来算。
权重值：归一化特征向量， 将特征向量的各个分量除以其和，使得分量之和为1。

最大特征根

特征根（或特征值）是线性代数中的概念，对于判断矩阵 $A$ ，特征根 $\lambda$ 满足以下方程：

A \mathbf{w} = \lambda \mathbf{w}

其中， $\mathbf{w}$ 是特征向量。

最大特征根的计算公式为：

λ_{max}= (1/n)∑_{i=1}^{n}(Aw)_{i}/w_{i}

这个公式的推导基于以下几点：

特征值定义：对于特征向量 $w$ ，有 $Aw = \lambda_{\text{max}} w$ ，因此每个分量满足 $(Aw)_i = \lambda_{\text{max}} w_i$ 。
近似计算：由于 $w$ 是一个近似的特征向量， $(Aw)_i / w_i$ 近似于 $\lambda_{\text{max}}$ 。通过对所有分量求平均，可以得到一个对 $\lambda_{\text{max}}$ 的估计。

一致性比率（CR）

核心问题： AHP 的核心在于通过构建判断矩阵来比较不同因素之间的相对重要性。然而，人们的判断往往存在一定程度的不一致性。例如，如果 A 比 B 重要，B 比 C 重要，那么逻辑上 A 应该比 C 更重要。但人们在实际判断中可能出现 A 不如 C 重要的情况，这就产生了不一致性。

因为一致性矩阵有如下性质：

如果一个判断矩阵是一致的，那么它的最大特征值正好等于矩阵的阶数n；
如果不一致，则最大特征值会大于n。

因此，通过计算最大特征值可以评估判断矩阵的一致性比率（Consistency Ratio, CR），进而检验判断矩阵是否可接受。

计算步骤如下：

计算一致性指标（CI） ：
- 一致性指标的公式为：
  $\text{CI} = \frac{\lambda_{\text{max}} - n}{n - 1}$
- 其中， $n$ 是判断矩阵的阶数（即矩阵的维度）。
查找随机一致性指标（RI） ：
- 随机一致性指标是通过大量随机矩阵计算得到的平均一致性指标，常用的RI值如下：

计算一致性比率（CR） ：
- 一致性比率的公式为：
  $\text{CR}= \frac{\text{CI}}{\text{RI}}$
- 如果CR小于0.1，则判断矩阵具有满意的一致性。

计算判断矩阵一致性比率示例

假设有一个3x3的判断矩阵 $A$ ：

A = \begin{bmatrix} 1 & 3 & 0.5 \\ \frac{1}{3} & 1 & \frac{1}{7} \\ 2 & 7 & 1 \end{bmatrix}

计算特征值和特征向量：
- 计算特征向量
  - 方法一：几何平均法计算特征向量
    - 计算每行元素的乘积 Mi
      - M₁ = 1 × 3 × 0.5 = 1.5
      - M₂ = 1/3 × 1 × 1/7 ≈ 0.0476
      - M₃ = 2 × 7 × 1 = 14
    - 计算每行乘积的n次方根 Wi（n=3）
      - W₁ = ∛1.5 ≈ 1.1447
      - W₂ = ∛0.0476 ≈ 0.3615
      - W₃ = ∛14 ≈ 2.4101
    - 归一化处理得到特征向量 wi
      
      总和：1.1447 + 0.3615 + 2.4101 = 3.9163
      
      特征向量w：
      - w₁ = 1.1447/3.9163 ≈ 0.2923
      - w₂ = 0.3615/3.9163 ≈ 0.0923
      - w₃ = 2.4101/3.9163 ≈ 0.6154
  - 方法二：算术平均法计算特征向量
    - 计算列和Sj
      - S₁ = 1 + 1/3 + 2 = 3.3333
      - S₂ = 3 + 1 + 7 = 11
      - S₃ = 0.5 + 1/7 + 1 = 1.6429
    - 标准化矩阵（每个元素除以列和）
      $\begin{bmatrix} 0.3000 & 0.2727 & 0.3043 \\ 0.1000 & 0.0909 & 0.0870 \\ 0.6000 & 0.6364 & 0.6087 \end{bmatrix}$
    - 计算行平均值
      
      特征向量w：
      - w₁ = (0.3000 + 0.2727 + 0.3043)/3 ≈ 0.2923
      - w₂ = (0.1000 + 0.0909 + 0.0870)/3 ≈ 0.0926
      - w₃ = (0.6000 + 0.6364 + 0.6087)/3 ≈ 0.6150
- 计算最大特征根
  
  $λ_{max} = \frac{1}{n}\sum_{i=1}^n \frac{(Aw)_i}{w_i}$
  1. 计算Aw的值：
    1
    2
    3
    [1 3 0.5] [0.2923] [0.8769]
    [1/3 1 1/7] [0.0923] = [0.2776]
    [2 7 1 ] [0.6154] [1.8461]
  2. 计算(Aw)i/wi：
    - (Aw)₁/w₁ = 0.8769/0.2923 = 3
    - (Aw)₂/w₂ = 0.2776/0.0923 = 3.0076
    - (Aw)₃/w₃ = 1.8461/0.6154 =2.9998
  3. 计算λmax：
    $λ_{max}= (3 + 3.0076 + 2.9998)/3 ≈ 3.0025$
计算CI： $\lambda_{\text{max}}= 3.0025$ ，则
$\text{CI}= \frac{3.0025 - 3}{3 - 1}= 0.00125$
查找RI：对于 $n = 3$ ，RI = 0.52。

计算CR：
$\text{CR}= \frac{\text{CI}}{\text{RI}}= \frac{0.00125}{0.52}\approx 0.0024$
因为CR < 0.1，判断矩阵具有满意的一致性。

通过这些步骤，你可以计算AHP中的特征向量、特征根和一致性比率，从而确保决策过程的合理性和一致性。

编程实现

python

import numpy as np


def ahp_consistency_check(A):
    # 获取矩阵的大小
    n, m = A.shape

    # 求出最大特征值及对应的特征向量
    eigvals, eigvecs = np.linalg.eig(A)
    max_eig = np.max(eigvals)

    # 计算一致性指标 CI
    CI = (max_eig - n) / (n - 1)

    # 随机一致性指标 RI
    RI = [
        0.0,
        0.0001,
        0.52,
        0.89,
        1.12,
        1.26,
        1.36,
        1.41,
        1.46,
        1.49,
        1.52,
        1.54,
        1.56,
        1.58,
        1.59,
    ]

    # 计算一致性比例 CR
    CR = CI / RI[n-1]

    # 输出结果
    print(f"一致性指标 CI = {CI:.4f}")
    print(f"一致性比例 CR = {CR:.4f}")

    if CR < 0.10:
        print("因为 CR < 0.10，所以该判断矩阵的一致性可以接受！")
    else:
        print("注意：CR >= 0.10，因此该判断矩阵需要进行修改！")


A = np.array([[1, 3, 0.5], [1 / 3, 1, 1 / 7], [2, 7, 1]])


# 调用函数进行一致性检验
ahp_consistency_check(A)

matlab

A = [
    1, 3, 0.5;
    1/3, 1, 1/7;
    2, 7, 1
]
[n, m] = size(A); %获取A的行列
%求出最大特征值及对应的特征向量
[V, D] = eig(A); %V是特征向量 D是特征值构成的对角矩阵
Max.eig = max(max(D)); %先求出每一列的最大值，再求最大值中的最大值
CI = (Max.eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
%经验值, 当判断矩阵多于n = 15
%这里n=2时，CI一定要变得很小，所以CI=0。我们为了避免分母为0，特设的第二个元素成为了很接近0的正数
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
    disp('因为CR<0.10，所以该判断矩阵的一致性可以接受！');
else
    disp('注意：CR >= 0.10，因此该判断矩阵需要进行修改！');
end

‍

例子：选择旅行目的地

假设你计划一次旅行，有三个目的地可供选择：A、B 和 C。你需要考虑以下四个因素：

旅游成本 (Cost)
景点吸引力 (Attractions)
住宿条件 (Accommodation)
餐饮质量 (Food)

1. 建立层次结构模型:

目标层: 选择最佳旅行目的地
准则层: 旅游成本 (C1)、景点吸引力 (C2)、住宿条件 (C3)、餐饮质量 (C4)
方案层: 目的地 A、目的地 B、目的地 C

2. 构造判断矩阵:

准则层判断矩阵:

准则	C1 (成本)	C2 (景点)	C3 (住宿)	C4 (餐饮)
C1 (成本)	1	1/3	1/2	1
C2 (景点)	3	1	2	3
C3 (住宿)	2	1/2	1	2
C4 (餐饮)	1	1/3	1/2	1

方案层判断矩阵 (以 C1 成本为例):

目的地 (成本)	A	B	C
A	1	2	4
B	1/2	1	2
C	1/4	1/2	1

方案层判断矩阵 (以 C2 景点为例):

目的地 (景点)	A	B	C
A	1	1/3	1/2
B	3	1	2
C	2	1/2	1

方案层判断矩阵 (以 C3 住宿为例):

目的地 (住宿)	A	B	C
A	1	1/2	1
B	2	1	2
C	1	1/2	1

方案层判断矩阵 (以 C4 餐饮为例):

目的地 (餐饮)	A	B	C
A	1	1	1/2
B	1	1	1/2
C	2	2	1

3. 计算权重向量和一致性检验:

使用特征值法计算每个判断矩阵的最大特征值和特征向量，并进行归一化处理，得到权重向量。然后计算 CI 和 CR，进行一致性检验。这里省略具体计算过程，假设所有判断矩阵都通过了一致性检验 (CR < 0.1)。

准则层权重向量 (假设): W_criteria = [0.15, 0.45, 0.30, 0.10]
方案层权重向量 (假设):
- W_cost = [0.57, 0.29, 0.14]
- W_attractions = [0.14, 0.54, 0.32]
- W_accommodation = [0.25, 0.50, 0.25]
- W_food = [0.25, 0.25, 0.50]

4. 计算综合权重:

将方案层相对于每个准则的权重与该准则相对于目标的权重相乘，然后将各个准则的结果相加：

目的地 A: 0.15 * 0.57 + 0.45 * 0.14 + 0.30 * 0.25 + 0.10 * 0.25 = 0.2485
目的地 B: 0.15 * 0.29 + 0.45 * 0.54 + 0.30 * 0.50 + 0.10 * 0.25 = 0.4615
目的地 C: 0.15 * 0.14 + 0.45 * 0.32 + 0.30 * 0.25 + 0.10 * 0.50 = 0.2900

5. 做出决策:

根据综合权重，目的地 B 的得分最高 (0.4615)，其次是目的地 C (0.2900)，最后是目的地 A (0.2485)。因此，根据 AHP 分析结果，你应该选择目的地 B 作为你的旅行目的地。

层次分析法分析代码

Python 代码

import numpy as np

def ahp(criteria_matrix, alternative_matrices):
    """
    AHP 层次分析法计算

    Args:
        criteria_matrix: 准则层判断矩阵
        alternative_matrices: 方案层判断矩阵列表

    Returns:
        综合权重向量
    """

    def calculate_weight(matrix):
        """计算权重向量和一致性检验"""
        eigenvalues, eigenvectors = np.linalg.eig(matrix)
        max_eigenvalue = np.max(eigenvalues)
        max_eigenvector = eigenvectors[:, np.argmax(eigenvalues)].real
        normalized_weight = max_eigenvector / np.sum(max_eigenvector)

        # 一致性检验
        n = matrix.shape[0]
        RI = [0, 0, 0.58, 0.90, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49]  # 10阶以内的RI值
        CI = (max_eigenvalue - n) / (n - 1)
        CR = CI / RI[n - 1] if n > 1 else 0

        if CR < 0.1:
            print(f"判断矩阵通过一致性检验 (CR={CR:.4f})")
        else:
            print(f"判断矩阵未通过一致性检验 (CR={CR:.4f})，需要进行调整")

        return normalized_weight

    # 计算准则层权重
    criteria_weight = calculate_weight(criteria_matrix)
    print(f"准则层权重: {criteria_weight}")

    # 计算方案层权重
    alternative_weights = []
    for matrix in alternative_matrices:
        alternative_weights.append(calculate_weight(matrix))
        print(f"方案层权重: {calculate_weight(matrix)}")

    # 计算综合权重
    final_weight = np.dot(np.array(alternative_weights).T, criteria_weight)

    return final_weight

# 准则层判断矩阵
criteria_matrix = np.array([
    [1, 1/3, 1/2, 1],
    [3, 1, 2, 3],
    [2, 1/2, 1, 2],
    [1, 1/3, 1/2, 1]
])

# 方案层判断矩阵
alternative_matrices = [
    np.array([[1, 2, 4], [1/2, 1, 2], [1/4, 1/2, 1]]),  # 成本
    np.array([[1, 1/3, 1/2], [3, 1, 2], [2, 1/2, 1]]),  # 景点
    np.array([[1, 1/2, 1], [2, 1, 2], [1, 1/2, 1]]),  # 住宿
    np.array([[1, 1, 1/2], [1, 1, 1/2], [2, 2, 1]])   # 餐饮
]

# 计算综合权重
final_weight = ahp(criteria_matrix, alternative_matrices)

# 输出结果
print(f"综合权重: {final_weight}")
print(f"最佳方案: 目的地 {'ABC'[np.argmax(final_weight)]}")

MATLAB 代码

function final_weight = ahp(criteria_matrix, alternative_matrices)
% AHP 层次分析法计算
%
% Args:
%     criteria_matrix: 准则层判断矩阵
%     alternative_matrices: 方案层判断矩阵列表，cell类型
%
% Returns:
%     综合权重向量

    function [normalized_weight, CR] = calculate_weight(matrix)
        % 计算权重向量和一致性检验
        [eigenvectors, eigenvalues] = eig(matrix);
        [max_eigenvalue, max_index] = max(diag(eigenvalues));
        max_eigenvector = eigenvectors(:, max_index);
        normalized_weight = max_eigenvector / sum(max_eigenvector);

        % 一致性检验
        n = size(matrix, 1);
        RI = [0, 0, 0.58, 0.90, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49]; % 10阶以内的RI值
        CI = (max_eigenvalue - n) / (n - 1);
        CR = CI / RI(n);

        if CR < 0.1
            fprintf('判断矩阵通过一致性检验 (CR=%.4f)\n', CR);
        else
            fprintf('判断矩阵未通过一致性检验 (CR=%.4f)，需要进行调整\n', CR);
        end
    end

    % 计算准则层权重
    [criteria_weight, ~] = calculate_weight(criteria_matrix);
    fprintf('准则层权重: %s\n', mat2str(criteria_weight',4));

    % 计算方案层权重
    alternative_weights = [];
    for i = 1:length(alternative_matrices)
        [alternative_weight, ~] = calculate_weight(alternative_matrices{i});
        alternative_weights = [alternative_weights, alternative_weight];
        fprintf('方案层权重: %s\n', mat2str(alternative_weight',4));
    end

    % 计算综合权重
    final_weight = alternative_weights * criteria_weight;
end

% 准则层判断矩阵
criteria_matrix = [
    1, 1/3, 1/2, 1;
    3, 1, 2, 3;
    2, 1/2, 1, 2;
    1, 1/3, 1/2, 1
];

% 方案层判断矩阵
alternative_matrices = {
    [1, 2, 4; 1/2, 1, 2; 1/4, 1/2, 1],  % 成本
    [1, 1/3, 1/2; 3, 1, 2; 2, 1/2, 1],  % 景点
    [1, 1/2, 1; 2, 1, 2; 1, 1/2, 1],  % 住宿
    [1, 1, 1/2; 1, 1, 1/2; 2, 2, 1]   % 餐饮
};

% 计算综合权重
final_weight = ahp(criteria_matrix, alternative_matrices);

% 输出结果
fprintf('综合权重: %s\n', mat2str(final_weight',4));
[~, max_index] = max(final_weight);
fprintf('最佳方案: 目的地 %s\n', char('A' + max_index - 1));

疑难解惑

二级指标如何计算权重？

不论是准测层，还是方案层，均是一样的数据输入方式，并且进行权重计算。准测层单独录入判断矩阵进行计算权重即可。如果准测层和方案层均均测量了权重，可以手工进行相乘计算得到各方案层最终的权重值。

比如有3个一级指标分别是A,B,C；A对应着A1,A2,A3; B对应着B1,B2,B3,B4; C对应着C1,C2,C3,C4；那么A1,A2,A3进行一次得到权重；B1,B2,B3,B4进行一次得到权重；C1,C2,C3,C4进行一次得到权重。 A,B,C也一定需要有数据才可以，单独进行一次得到权重。

最终比如A1,A2,A3的权重等于A的权重乘上自己的权重。

下面例子：智能刹车辅助系统的综合权重为0.274（二级指标权重）*0.366（一级指标权重）=0.100284

《基于AHP层次分析法的智能婴儿手推车设计研究》

多个专家打分如何处理？

如果有多个专家，通常的做法将多个专家打分进行计算平均值，进行一次AHP层次分析即可，而不是每个专家都进行一次AHP层次分析。

如果有多个专家进行打分，然后进行AHP，1个专家有1个打分矩阵。那么首先需要进行‘平均’处理，此处的平均为‘几何平均’（非‘算术平均’），如下所述：

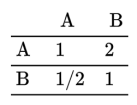
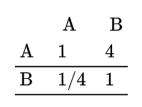
上面为2个专家的打分矩阵，那么进行‘几何平均’如下(对应值相乘然后取1/N次方，N表示专家数量)，‘几何平均’后得到一个汇总矩阵，然后SPSSAU分析时使用该矩阵进行AHP分析就好。

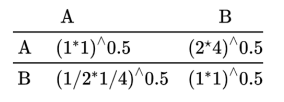
AHP层次分析法与自己计算不一致？

AHP层次分析法有多种方法进行计算，区别在于个别计算步骤上有区别但结果基本完全一致，SPSSAU默认以和积法作为计算方法。
问卷量表题是否可以计算AHP权重？

AHP层次分析法计算权重只需要输入判断矩阵即可。如果是问卷量表题，可手工计算出研究项之间的相对重要性，得到判断矩阵，最终完成权重计算；比如有想计算5个量表题的权重，可分为三个步骤进行。第一步：计算5个量表题平均值；第二步：计算此5个平均值的相对大小（即判断矩阵可直接计算出来）；第三步：录入判断矩阵，开始分析。

如果对于分析使用的原始数据格式有疑问，请参考下面链接说明：https://www.spssau.com/helps/otherdocuments/methodsdataformat.html
RI值与参考文献不一致？

平均随机一致性指标RI值通过随机值工程计算得到，本身就带有随机性，但此种随机性体现在数值上仅有非常细微的区别，并且是正常且正确的。

SPSSAU使用的RI指标值参考文献如下：

洪志国, 李焱, 范植华, et al. Caculation on High-ranked R I of Analytic Hierarchy Process%层次分析法中高阶平均随机一致性指标(RI)的计算[J]. 计算机工程与应用, 038(12):45-47，150.
AHP整体一致性检验？

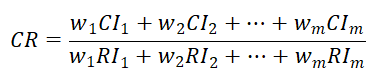
如果需要计算整体一致性，此种情况基于具有层次结构的AHP计算，其计算公式如上图。上式中涉及的m, w, CI和RI均是指‘高层次’（比如准则层）对应的指标数据，m为准则层指标数量，w为准则层指标对应的权重值，CI和RI值为分别多次AHP的结果，比如‘第1个准则层指标’对应方案层进行AHP时得到的数据。CR的检验标准为CR<0.1即说明具有整体一致性。

参考

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。